
Poggendorff Illusion

That is Johann Christian Poggendorff who was German physicist. Poggendorff noticed an illusion in an article submitted to a journal that he was editing. Look at the two oblique lines below:
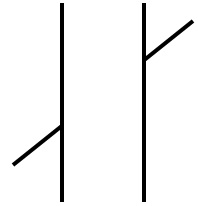
Do the two oblique lines appear collinear? That is, do they appear to fall on the same line? Most people perceive the oblique line on the right as higher than it would be if it was collinear with the oblique line on the left.
There are several theories as to why the Poggendorff illusion occurs. One theory claims that we misperceive the angles formed by the oblique lines and the lines defining the gap. In particular this explanation claims that we overestimate the size of acute angles and underestimate the size of obtuse angles. If this is true, then the oblique lines in the example illusion above should appear more horizontal. In the activity below, if you adjust the slope of the oblique line so the line is closer to horizontal, the stength of the illusion should get smaller and smaller until it completely goes away for a horizontal line.
A second theory claims that the illusion arises because we are misapplying depth cues. According to this theory, the oblique lines are perceived as receding into the distance (like a single railroad rail) and the gap is seen as being closer to the observer than the lines (it is perceived as occluding the oblique lines and must therefore be closer). If you perceive the illusion in this way, then the visual system interprets the angles between the oblique lines and the gap as right angles. This is easier to see when you look at the following image.
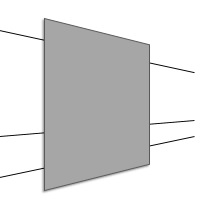
One of the more recent theories is by Howe, Yang and Purves (2005). Howe et al. argue that the illusion arises because of our experiences with lines in nature that have been occluded by objects. That is, the illusion arises because of our experiences and it leads to more veridical perception of real world objects. The theory states that occluded objects can change direction behind the occluder or even stop behind the occluder. When (if) they emerge from the other side of the occluder, they may or may not be collinear with when they entered behind the occluder. Thus, there is a range of probable line segments. Experience tells us how probable each line that could exit the occlusion is and we should pick the line that is most probable. Based on analysis of real world scenes, Howe et al. conclude that the most probable lines are biased in such a way that the Poggendorff illusion should arise.
The Activity:
Below you will see the Poggendorff illusion. Your task is to drag the "Right segment vertical position" slider left (to lower the segment) or right (to raise the segment) until it appears to be collinear with the segment to the left. When you think the two oblique lines are collinear, you can uncheck the "Show gap vertical lines" and / or, check the "Show line in gap" and/or slide the "Gap size" slider all the way to the left to see how well you did. If you were perfect, the two line segments should exactly line up with each other.
Here are some things to try. How do they influence the strength of the illusion?
Right segment vertical position:
Gap size:
Line slope:
Show gap vertical lines:
Show line in gap:
Howe, C. Q., Yang, Z., & Purves, D. (2005). The Poggendorff illusion explained by natural scene geometry. Proceedings of the National Academy of Sciences of the United States of America, 102, 7707-7712. http://dx.doi.org/10.1073/pnas.0502893102