Metamers

Background:

Two lights are metamers if their spectral properties (wavelengths and amplitudes) are different yet they are perceptually identical. The fact that a light of any given visible wavelength and intensity can be metamerically matched by adjusting the intensity of the additive mixture of three other lights (whose wavelengths are fairly widely spaced across the visible spectrum) is strong evidence that normal human color vision is trichromatic -- that is, that it is based on three types of photoreceptors, the S, M and L cones.

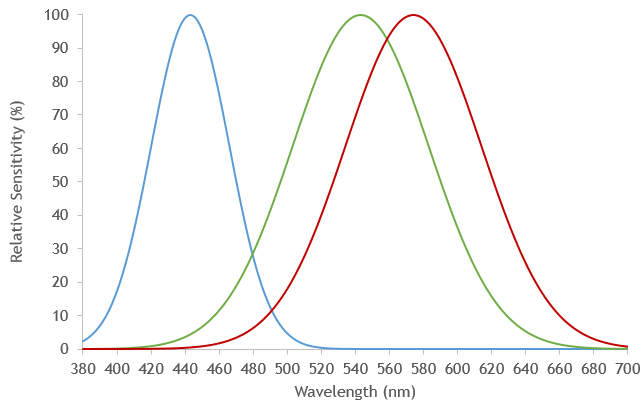
Monochromatism is a visual disorder in which a person has only one type of cone and therefore is completely color blind. Such a person perceives the world in shades of gray and will always confuse the wavelength of light with the intensity of the light. Why? Whether a cone signals the presence of light or not depends on two factors -- how much light is present (the brighter the light, the more likely the cone is to signal that the light is present) and the wavelength of the light. Each type of cone (and the rods) prefer one wavelength of light the most and are most likely to absorb light with that wavelength. Each type of cone (and the rods) prefer, to a lesser extent, other similar wavelengths and are somewhat less likely to absorb light of those wavelengths. The farther the wavelength is from the preferred wavelength, the less and less likely the photoreceptor is to absorb ligth of that wavelength. If you plot the wavelength of light versus the sensitivity of a photoreceptor to that wavelength, you will get the spectral absorption curve for the photoreceptor. The spectral absorption curves are also known as spectral sensitivity functions. Below are spectral sensitivity functions for the three types of cones (the functions only approximate the real functions.)

For the above functions, the S-cones have a relative sensitivity of about 60% for a 466 nm light. That is, about 6 out of every 10 photons with a wavelength of 466 nm are absorbed by the S-cones. The S-cones also have a relative sensitivity of about 30% for 479 nm light. Shining a 466 nm wavelength light with an intensity of 10 (arbitrary units) on an S-cone will cause the same response as shining a 479 nm wavelength light with intensity of 20 on an S-cone. If the first case, the S-cone will absorb 60% of 10 = 0.6; in the second case, the S-cone will absorbe 30% of 20 = 0.6. S-cones by themselves cannot distinguish these two lights -- they are metamers. In general, a single cone type can confuse any two lights as long as you can adjust the intensity of one of the lights and the cone is sensitive to the wavelengths of both lights. This is a direct consequence of the univariance principle -- the cone does not know about the wavelength or intensity of the light -- it only knows that one (or more) photons have been absorbed.

Using a procedure analogous to population codes, the combined output of two cone systems will not confuse these two lights. The M-cones have a relative sensitivity of 16% for a 466 nm light and 28% for a 407 nm light. While the S-cone cannot distinguish the two lights, the S plus M cones can. The two lights are no longer metamers.

We can still make a metameric match to the 466 nm light with intensity 10. However, it cannot be done with a single other wavelength, no matter what intensity it is set to. To do so requires an additive mixture of two lights (of different wavelengths) whose intensities can be adjusted. The following table represents one (of many) metameric matches for the a visual system with only S- and M-cones:

The S-cones have a sensitivity of 36% for a 410 nm light and a sensitivity of 0% for 580 nm light. The M-cones have a sensitivity of 0% for a 410 nm light and a sensitivity of 65% for 580 nm light. Setting the 410 nm light to intensity 16.7 yields an activity level of 6.0 (I * λ sensitivity = 16.7 * 0.36 = 6.0) for the S-cones and an activity level of 0.0 (I * λ sensitivity = 16.7 * 0.00 = 0.0) for the M cones. Similarly, setting the 580 nm light to intensity 2.5 yields an activity level of 0.0 (2.5 * 0.00 = 0.0) for the S-cones and an activity level of 1.6 (2.5 * 0.65 = 1.6) for the M-cones. Thus, an additive mixture of a 410 nm light at intensity 16.7 and a 580 nm light at intensity 2.5 will be a metameric match for a 466 nm light at intensity 10 if only the S- and M-cone systems are considered.

While the additive mixture of the lights with 410 nm wavelength at intensity 16.7 and 580 nm wavelength at intensity 2.5 is a metameric match for the S- and M-cone systems, it is not a metameric match for all three cone systems. The L-cones are sensitive to the 580 nm light -- approximately 99% relative sensitivity. Thus, if we add the L-cones to the system, we can distinguish between the 466 nm light (which would have no activity in the L-cones) and the additive mixture of 410 nm and 580 nm lights (which would produce activity in the L-cones.) With three types of cones, three lights (of widely separated wavelengths) are needed to perform most metameric matches. Because humans with normal color vision require three lights to make a metameric match, we must have three distinct types of cones. That is, we are trichromatic.

The Activity:

Your task is to find metameric matches by changing the wavelength and/or intensity of up to three other lights. The activity defaults to showing the spectral sensitivity functions for each of the three types of cones -- the S-cone spectral sensitity function is shown in blue, the M-cone function is shown in green and the L-cone function is shown in red.

The to-be-matched light is represented as a black, dashed line extending upward from the X axis until it strikes each of the three distributions. Where it strikes each distribution, a horizontal dashed line is drawn to the Y-axis. The Y-axis value indicates how sensitivity that cone is to the to-be-matched light's wavelength. Coupled with the intensity of the to-be-matched line (given in the table under the functions), one can calculate how active each type of cone is to the to-be-matched light. Activity is the product of intensity (which is proportional to the number of photons shining on the cone per unit of time) and sensitivity.

In general, to make a metameric match in a trichromatic person, you need to be able to adjust the wavelength and/or intensity of three other lights. Those lights are indicated as "1", "2" and "3" in the table and with blue, green and red dashed lines in the diagram. Adjust the wavelength by moving the wavelength slider. Moving it to the left shortens the wavelength while moving it to the right lengthens the wavelength. Adjust the intensity by moving the intensity slider -- left makes the light more dim while right makes it brighter.

Finally, you can select which types of cones to use by checking or unchecking to the box to the right of each cone type.

Your task is to make metamers of the to-be-matched light by adjusting the wavelength and/or intensity of the three other lights.

• Verify that the univariance principle is correct. Turn off the S- and L-cones (or any two types of cones.) Adjust the wavelength and / or intensity of the active light until that light's activity matches the to-be-matched light's activity. Convince yourself that many such metameric matches are possible when a single type of cone is active. Using a single type of cone confuses wavelength and intensity.
• Use two types of cones (for example S- and M-) and try to make a metameric match by manipulating the wavelength and/or intensity of two lights. Often this is easy if you make the wavelength of one light relatively short (say 420 nm) so that only the S-cones are sensitive to it and make the wavelength of the other light relatively long (say 600 nm) so that only the M-cones are sensitive to it. Now adjust the intensity of first light until its activity matches the S-cone activity for the to-be-matched light and adjust the intensity of the second light until its activity matches the M-cone activity for the to-be-matched light.
• For the brave of heart, use all three types of cones and try to make a metameric match. This can be challenging. You can click on the "Show approximate 3-cone solution" to get a set of wavelengths and intensities that are very close to a perfect metameric match. Perfect metameric matches are possible, but they take longer to find.

The fact that humans with normal visual systems need to manipulate the intensities of three lights to create a metameric match to another light implies that we are trichromatic.

Use S Cones:     Use M Cones:     Use L Cones: